パラボラアンテナ(Parabolic Anntena)の形状を計算する。
焦点に電波の発信源を持ってくると、鋭い指向性が得られるらしい。
さて、今回の課題は、
(1)半径(R)、(2)(お椀の)深さ(δ)が与えられたとき、焦点位置(F)がどこにくるかを推定する計算式。パラボラアンテナは放物線(Y=aX2)を回転させた「お皿」だ。「お皿のカタチ」が与えられたら、焦点の位置を求める方法を得ることだ。
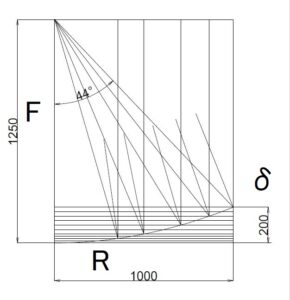
上の図の説明;
- 1000 x 1250の四角形の左下から、1000 x 200 への曲線が放物面。
- パラボラの半径:Rが1000mmなので、アンテナとしては直径2mを想定している。
- この放物面の接線に直行する垂線に対して、垂直に落ちてくる平行線(入射する電波のイメージ)と出射方向は鏡像になる。(入射角=出射角)
- これを放物面の何点かで描画し、上図の場合では1250mmが収束点となる。
放物線のグラフを眺めていたが、幾何学的に解けそうも無さそうだ。そこで、チカラ技ではあるが、Dとδのパラメータを振った放物線をエクセルで用意し、CADに注入、焦点位置(F)を推定した。
手っ取り早く結論;
となります。単位はmmでもmでもOK。
具体的な作業手順は以下のようなものです。宜しければ、下記リンクにお越しください。
複雑な形状を生成する作業は、CADにデータを注入すると、手間が少なくて済みます。これまで従事してきた、シミュレーション分野とか、半導体用フォトマスクの作成で、PCで出来ることはPCに任せようとしてきました。当時からだいぶ年月が経ちましたが、世の中は相変わらず進化し続けているようです。
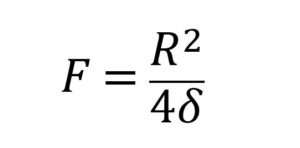
“パラボラ(1)-放物線の焦点位置を計算する” への2件のフィードバック
参考にさせていただきました。
まだ編集中につきまずはご連絡。
https://instagram.com/cybercatzz?igshid=YmMyMTA2M2Y=
宜しければお気づきの点などお知らせ下さい。
こちら(h-sol.jp)はあまり更新しておらず、雑文を下記に集積してます。
https://www.sub.h-sol.jp/zakki-cho/